Index Misconceptions [TSQL Tuesday #026 – Second Chances]
T-SQL Tuesday #26 is hosted by David Howard (blog|twitter). This month’s topic is “Second Chances”.
Index Misconceptions
The topic this month is "Second Chances" which means that we can write about anything, we would have liked to write about before but didn't get to. Well, not really anything, but any of the 25 previos T-SQL Tuesday topics. I picked two topics: Indexes by Michael Swart and Misconceptions in SQL Server by Sankar Reddy.
Misconception: SQL Server Indexes are binary trees
I keep running into articles that claim that SQL Server internally uses a binary tree to build it's indexes. That however is incorrect and I would like to use this opportunity to clear things up a little.
SQL Server stores its tables (to be exact: table partitions) in a format that is called a HoBT. HoBT stands for "Heap or B-Tree". A Heap is used for tables without a clustered index. A B-Tree is used for all clustered and nonclustered indexes. If you lock up the word B-Tree on Wikipedia, the first sentence states: "Not to be confused with Binary tree."
The B in B-Tree is often said to stand fo "Balanced". However, when Rudolf Bayer and Ed McCreight at Boeing invented the B-Tree in 1971, they did not specify the meaning of the B at all.
Speculations include Balanced, Bushy, Bayer and Boeing (see again Wikipedia).
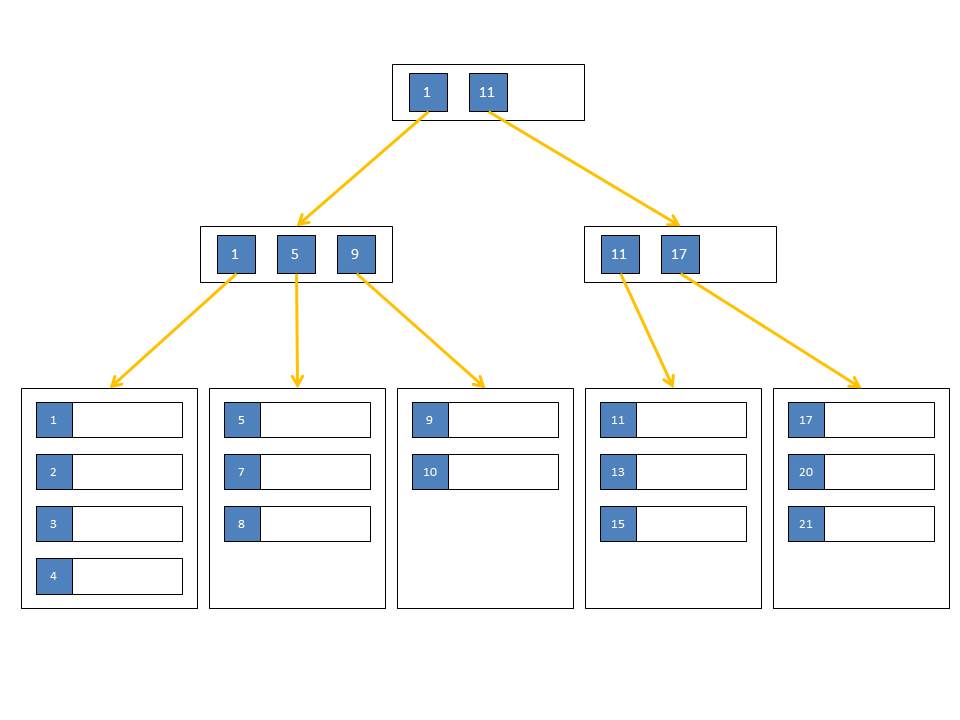
SQL Server is not using a plain B-Tree but instead a variation called a B+Tree. The main difference to a B-Tree is, that in a B+Tree the actual data is only stored in the leaf nodes with all other nodes containing only key values. In B-Trees the data is distributed over all levels.
So, let's take a look under the covers to see the structure for ourselves. First lets create a table to play with:
(
Id INT IDENTITY(1, 1) ,
V1 CHAR(795) ,
F1 CHAR(7254) ,
CONSTRAINT PK_IdxTst1 PRIMARY KEY CLUSTERED( Id, V1 )
) ;
[/sql]
The table has a 4 byte (INT) identity column and two fixed length CHAR columns. The Clustered Index key contains the Id and the 795 byte, a total of 799 bytes. The full row contains an additional 7254 bytes for a total row data size of 8053 bytes. Each row when stored contains some meta information and for this table this additional information is 7 bytes per row, which brings us to a total of 8060 bytes for each row. This is the maximum number of bytes that one row is allowed to take (we are excluding LOB data from this exercise). This row size will make sure that there is always only one row per page.
To look at the structure of the table we are going to use the sys.dm_db_index_physical_stats dmf:
FROM sys.dm_db_index_physical_stats(DB_ID(),OBJECT_ID('dbo.IdxTst1'),NULL,NULL,'DETAILED');
[/sql]
This query returns one row for every level of every B+Tree for the dbo.IdxTst1 table. As the table is not partitioned and contains only one index (the clustered index), the query in our case returns only information about this one index.
After inserting one row into the table the query returns the following result set:
| index_type_desc | Alloc_unit_type_desc | index_depth | index_level | page_count | record_count | avg_record_size_in_bytes |
|---|---|---|---|---|---|---|
| CLUSTERED INDEX | IN_ROW_DATA | 1 | 0 | 1 | 1 | 8060 |
The B+Tree has so far only one level (index_level = 0), contains 1 node (page_count = 1) and 1 record within that node. The record has the expected size of 8060 bytes.
To insert a second row SQL Server needs to create a new page (node), as each page can hold only one row. With now two data pages we also need a new root page that links to the data pages:
| index_type_desc | Alloc_unit_type_desc | index_depth | index_level | page_count | record_count | avg_record_size_in_bytes |
|---|---|---|---|---|---|---|
| CLUSTERED INDEX | IN_ROW_DATA | 2 | 0 | 2 | 2 | 8060 |
| CLUSTERED INDEX | IN_ROW_DATA | 2 | 1 | 1 | 2 | 806 |
As expected, the B+Tree has now two levels: Index_level 0 with 2 pages holding one row of 8060 bytes each, and index_level 1 for the root page which holds two records of 806 bytes each – one for each level 0 page. The 806 bytes contain the 799 byte key value plus the pointer to the data page for this key value.
With a key storage size of 806 a page can hold 10 different values, so lets insert an other 8 rows to check:
| index_type_desc | Alloc_unit_type_desc | index_depth | index_level | page_count | record_count | avg_record_size_in_bytes |
|---|---|---|---|---|---|---|
| CLUSTERED INDEX | IN_ROW_DATA | 2 | 0 | 10 | 10 | 8060 |
| CLUSTERED INDEX | IN_ROW_DATA | 2 | 1 | 1 | 10 | 806 |
And one more to force an additional page on index_level 1:
| index_type_desc | Alloc_unit_type_desc | index_depth | index_level | page_count | record_count | avg_record_size_in_bytes |
|---|---|---|---|---|---|---|
| CLUSTERED INDEX | IN_ROW_DATA | 3 | 0 | 11 | 11 | 8060 |
| CLUSTERED INDEX | IN_ROW_DATA | 3 | 1 | 2 | 11 | 806 |
| CLUSTERED INDEX | IN_ROW_DATA | 3 | 2 | 1 | 2 | 806 |
As predicted, we now have two pages on index_level 1 and a new root page on index_level 2. All the data (11 rows) is still stored in index_level 0 in 11 separate pages. All intermediate (and root) pages contain only key values (806 bytes).
The root page can hold 10 entries and each index_level 1 page can also hold 10 entries. That should allow us to insert an additional 89 rows into this table without requiring a fourth index level. So let's try it:
| index_type_desc | Alloc_unit_type_desc | index_depth | index_level | page_count | record_count | avg_record_size_in_bytes |
|---|---|---|---|---|---|---|
| CLUSTERED INDEX | IN_ROW_DATA | 4 | 0 | 100 | 100 | 8060 |
| CLUSTERED INDEX | IN_ROW_DATA | 4 | 1 | 24 | 100 | 806 |
| CLUSTERED INDEX | IN_ROW_DATA | 4 | 2 | 5 | 24 | 806 |
| CLUSTERED INDEX | IN_ROW_DATA | 4 | 3 | 1 | 5 | 806 |
What happened here? We have the expected 100 data rows and the corresponding 100 index_level 0 pages but instead of only 10 index_level 1 and one root page we have now 30 non leaf level pages spread over three levels.
The reason for this is that SQL Server, every time it requires a new page to insert a row, takes the page that should have contained the new row and splits its contents in half, leaving one half in the old page and moving the other half into the new page. After that it inserts the new row into the new page. This algorithm is used for all index pages, no matter of their index_level and independent of the value of the new row. (For leaf level pages SQL Server does not split the existing page if the position of the new row is the end of the table. It instead just adds a new empty page to the table and inserts the row in there. The example in this article hides this behavior as there is always only one row per data page.)
That algorithm leaves most of the intermediate index pages with only 5 rows, so after only 55 rows a new index level is required.
To reclaim that space lost space we need to rebuild the index:
[/sql]
Now the table structure looks as expected:
| index_type_desc | Alloc_unit_type_desc | index_depth | index_level | page_count | record_count | avg_record_size_in_bytes |
|---|---|---|---|---|---|---|
| CLUSTERED INDEX | IN_ROW_DATA | 3 | 0 | 100 | 100 | 8060 |
| CLUSTERED INDEX | IN_ROW_DATA | 3 | 1 | 10 | 100 | 806 |
| CLUSTERED INDEX | IN_ROW_DATA | 3 | 2 | 1 | 10 | 806 |
The FILLFACTOR of the index does not matter in this case as non data pages in an index are always completely filled during an index rebuild operation (unless PAD_INDEX = ON is also specified).
Conclusion
We did see that SQL Server uses a physical tree implementation that allows for more than two child nodes per tree node. We also confirmed that SQL Server stores only the key values in the non-leaf nodes. That are the two main characteristics of a B+Tree. It also clearly rules out the binary search tree format.
We also ran into a situation where most of the non-leaf levels of the index where only half filled. This is one of the disadvantages that come with the use of B+Trees. Usually this is however not a big issue, as the number of non leaf pages is usually small compared to the total number of pages. You might however want to keep an eye out for this behavior, especially if you ar dealing with overly wide keys, as we did in this example.
If you rather store you data as compact as possible you can do so by executing an index rebuild.
Additional Information
For further information about index internals with some nice graphics check out Michael Swart's Guts Of An Clustered Index, his contribution to his own SQL Saturday #10.