A Join A Day – Hash Join Limitations

Introduction

This is the twenty-eighth post in my A Join A Day series about SQL Server Joins. Make sure to let me know how I am doing or ask your burning join related questions by leaving a comment below.

There is one remaining join algorithm to dissect a little further: Today we are going to look at which situations can and which situations cannot be handled by the Hash Join operator.

Hash Join

For the Hash Join algorithm we again are going to look at all nine logical joins, each as equi- and as nonequi-join. The following is a list of example queries for each combination together with their execution plans, similar to the lists for the Loop Join algorithm and the Merge Join algorithm. Here too the list will only contain plain equi-join or nonequi-join scenarios and not include mixed cases, as those are handled similarly to equi-joins.

Cross Hash Join

Inner Hash Equi-Join

Left Hash Equi-Join

Right Hash Equi-Join

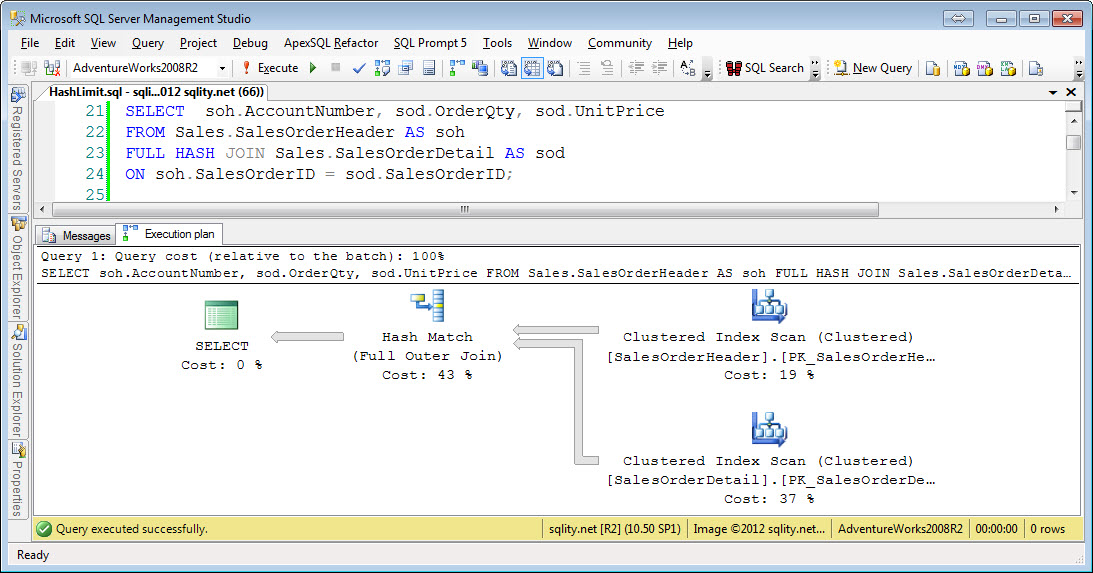
Full Hash Equi-Join

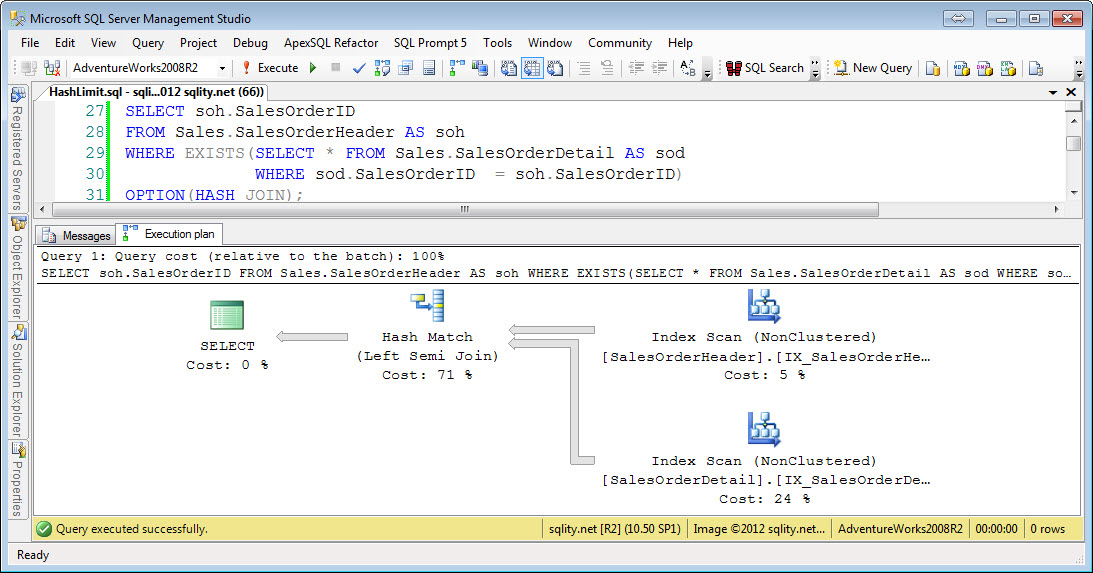
Left Semi Hash Equi-Join

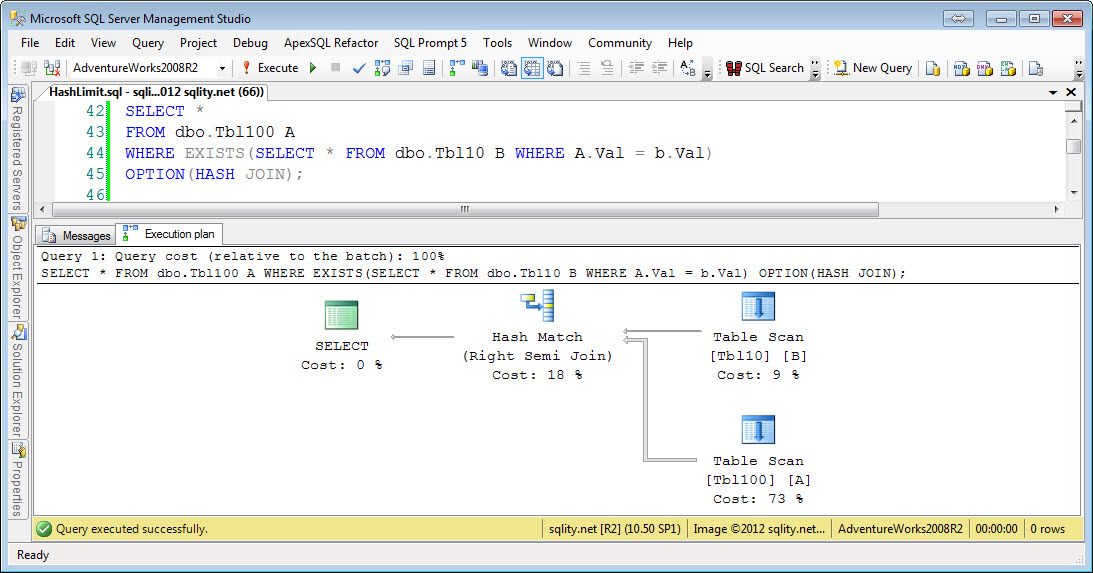
Right Semi Hash Equi-Join

This query and the Right Anti Semi Hash Equi-Join query are using the tables that we created in the article about the Loop Join algorithm.

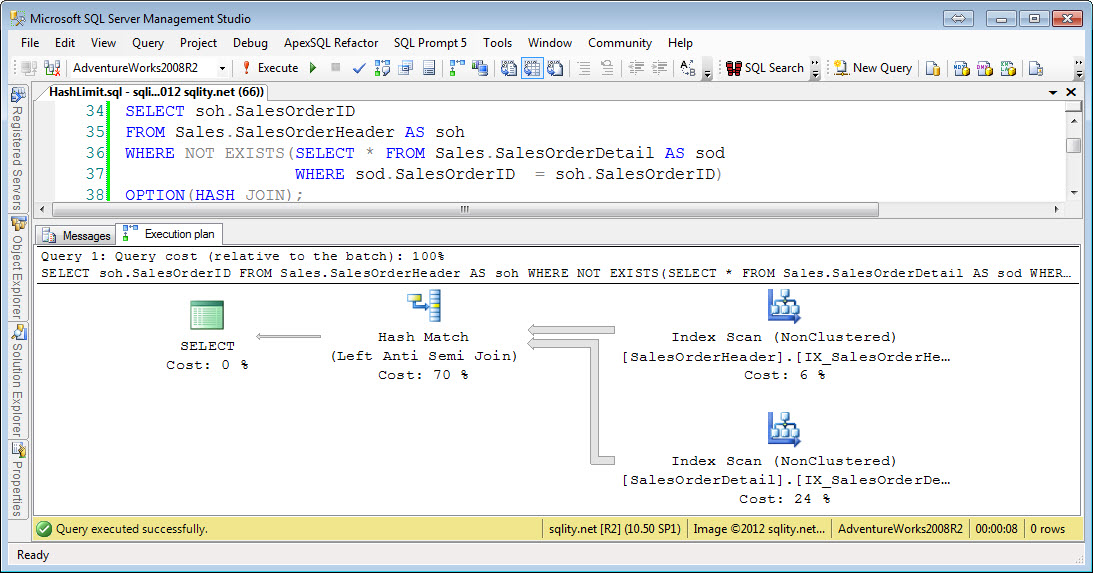
Left Anti Semi Hash Equi-Join

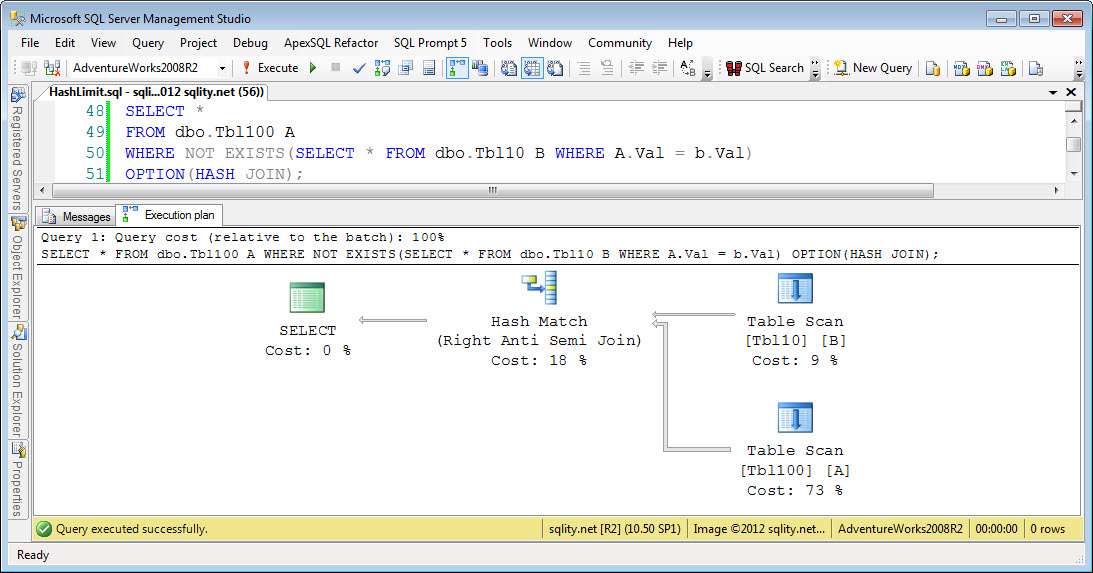
Right Anti Semi Hash Equi-Join

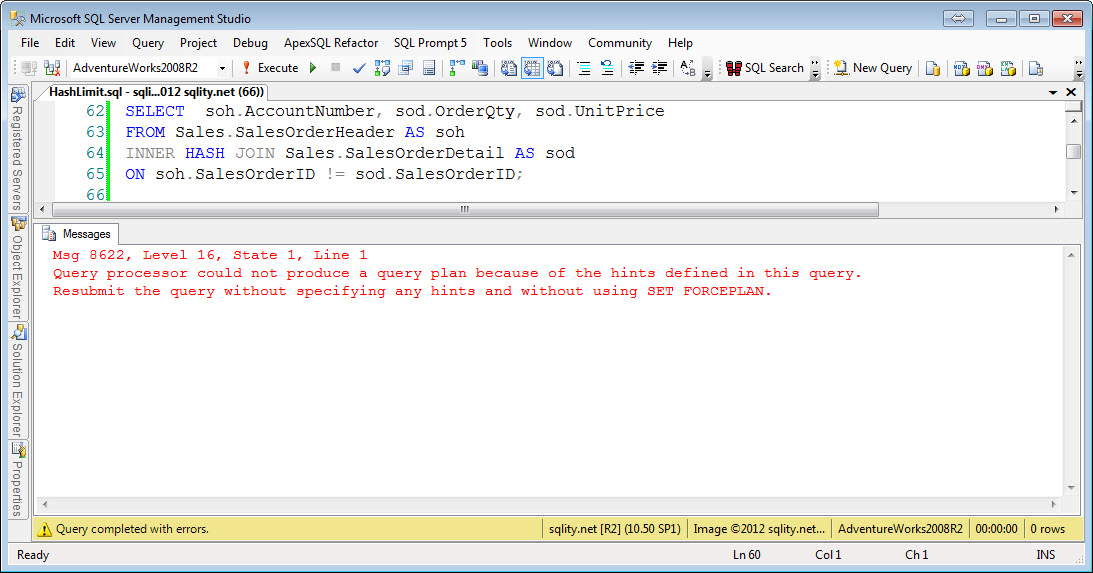
Inner Hash Nonequi-Join

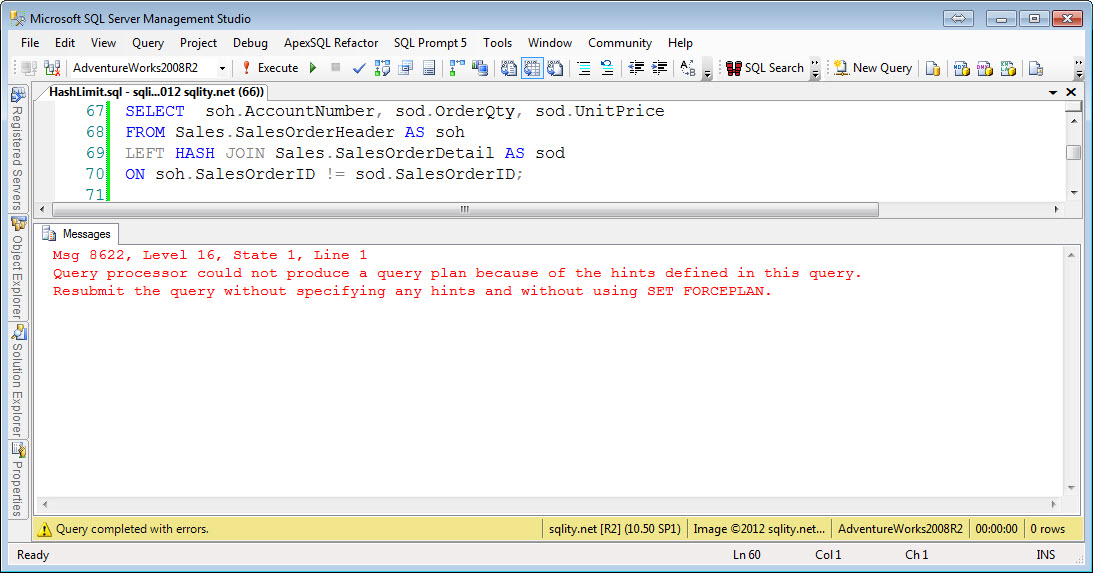
Left Hash Nonequi-Join

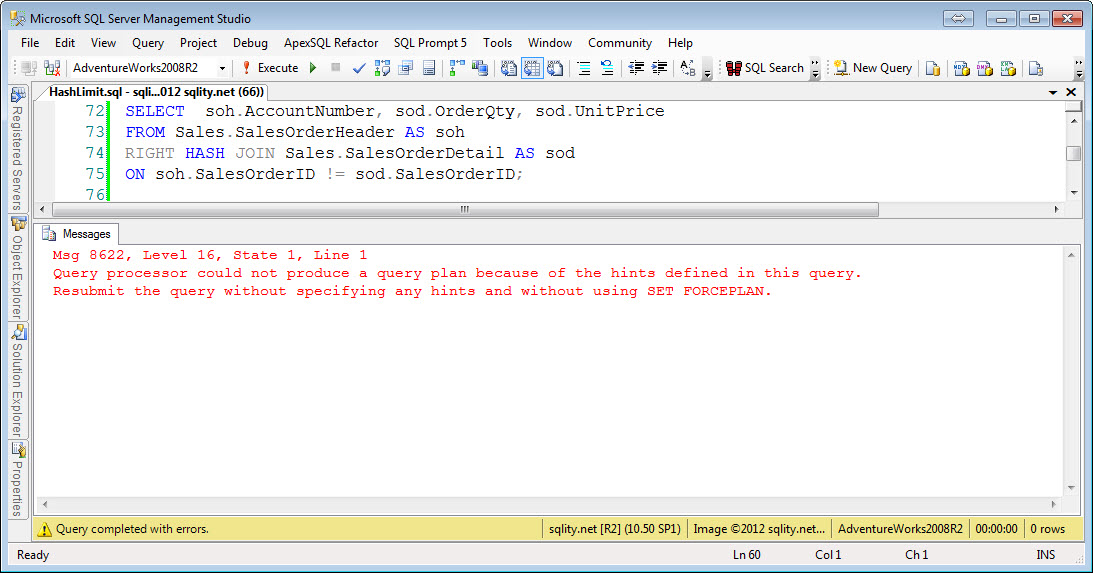
Right Hash Nonequi-Join

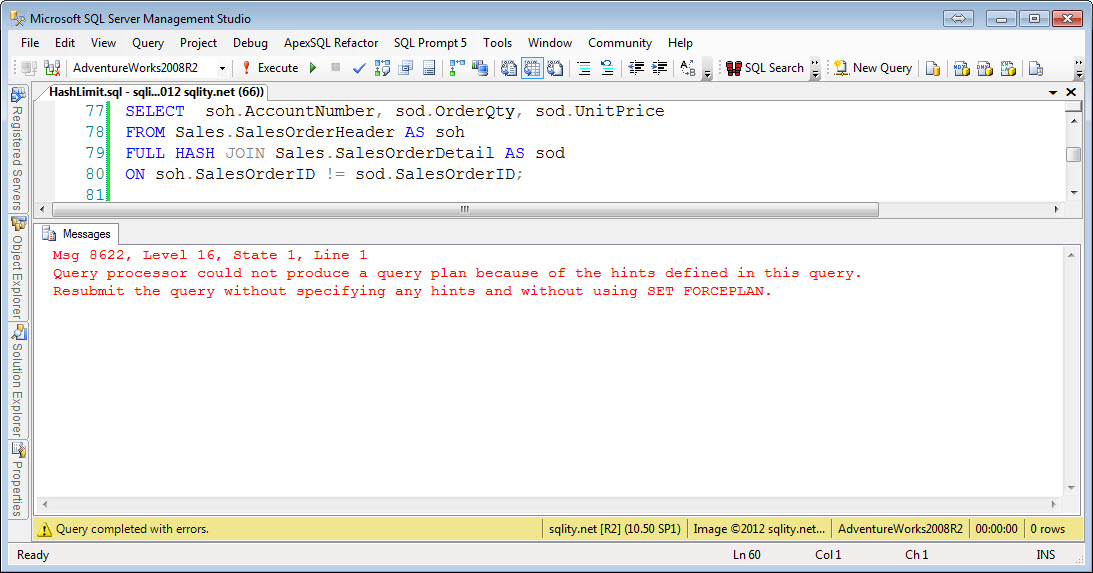
Full Hash Nonequi-Join

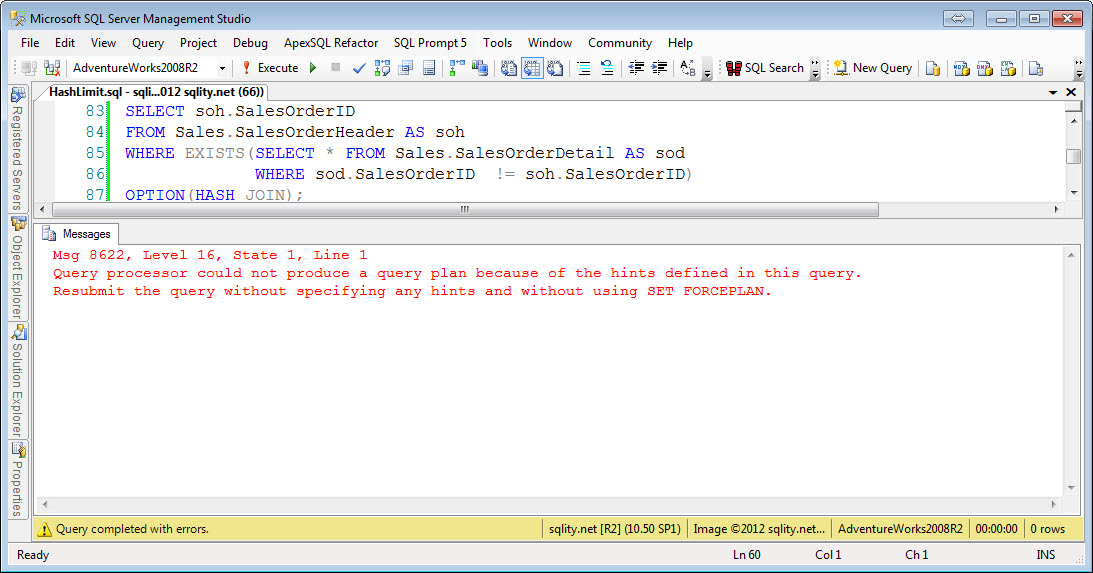
Left/Right Semi Hash Nonequi-Join

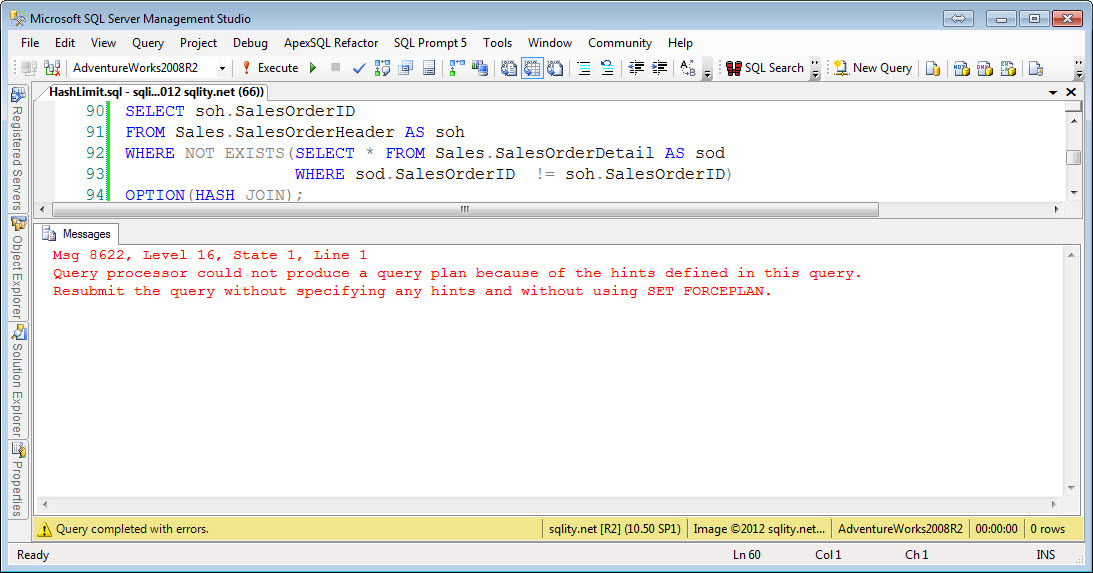
Left/Right Anti Semi Hash Nonequi-Join

Observations

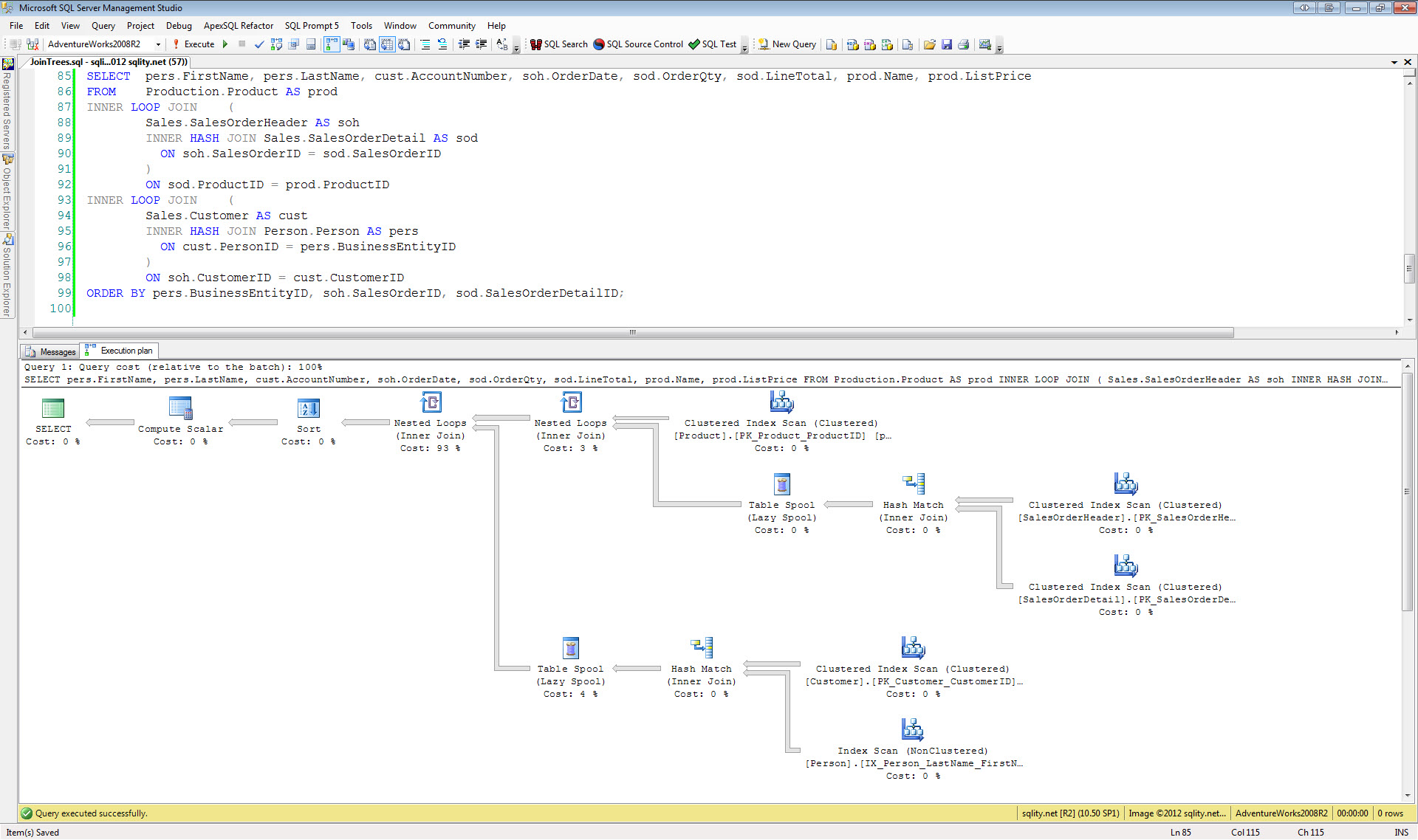
The Hash Join algorithm first builds a hash index for the left side input. For each row a hash value is calculated with a hash function. As we have seen in the article about the Hash Join algorithm, a good hash function needs to evenly distribute the rows across all available buckets. To achieve that a hash function is usually derived from a cryptographic function. Because of that, any sense of order gets lost when applying the function. That means that while you can compare two hash values with each other, the result of that comparison will be able to tell you only one thing: If the hash values do not match then the rows do not match either. In particular this means for an inequality comparison like "greater than" a hash index is of no value. So we would expect to see hash nonequi-joins to not be possible. The above example queries confirm that for all nonequi-joins including the join-condition-free cross join.

There are no real surprises in the examples above. Every equi-join condition can be handled by the Hash Join operator. Keep in mind however, that any "left" type query needs to keep track of all rows in the hash table that have been successfully matched to be able to retrieve the non-matched rows afterwards. This mark requires additional memory. While this is not a lot of addition memory, it might just be enough to cause the hash table not to fit into memory anymore causing the more expensive grace join algorithm to be used. So if you change a query from "inner join" to "outer join" and performance suffers significantly even though both queries use the Hash Join algorithm, this might just be the reason.

A Join A Day

This post is part of my December 2012 "A Join A Day" blog post series. You can find the table of contents with all posts published so far in the introductory post: A Join A Day – Introduction. Check back there frequently throughout the month.